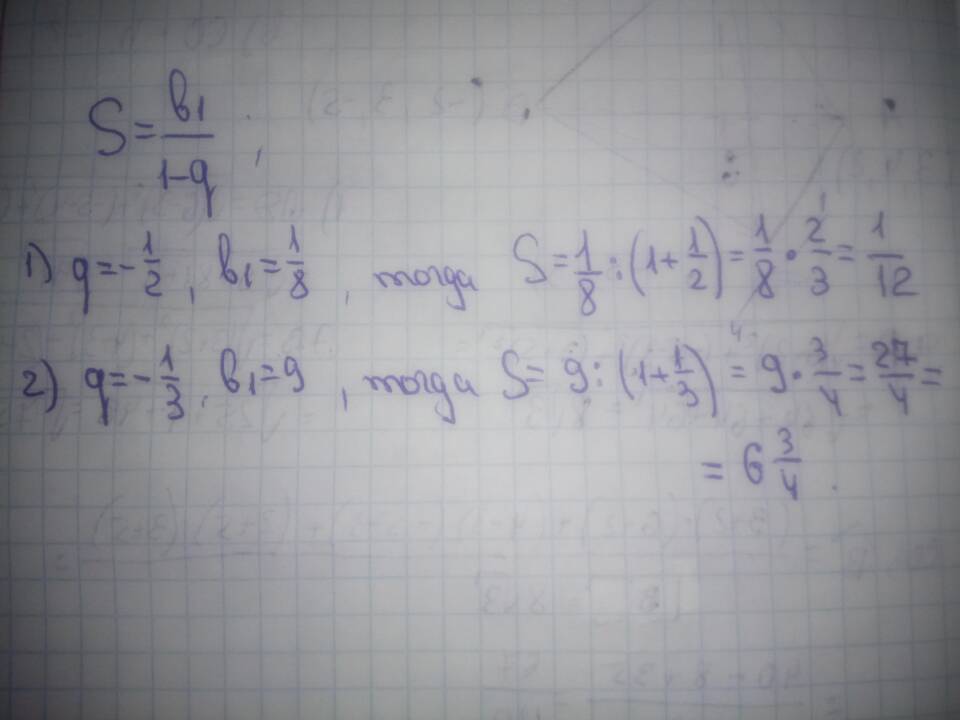Убывающая прогрессия - это числовая последовательность, в которой каждый следующий член меньше предыдущего. Рассмотрим методы расчета суммы членов такой прогрессии.
Содержание
Убывающая прогрессия - это числовая последовательность, в которой каждый следующий член меньше предыдущего. Рассмотрим методы расчета суммы членов такой прогрессии.
Основные понятия
| Термин | Обозначение | Описание |
| Первый член | a₁ | Начальное значение прогрессии |
| Знаменатель | q | Постоянное отношение соседних членов |
| Число членов | n | Количество суммируемых элементов |
Формулы для расчета суммы
Для конечной прогрессии
Sₙ = a₁(1 - qⁿ)/(1 - q), где |q| < 1
Для бесконечной прогрессии
S = a₁/(1 - q), где |q| < 1
Пошаговый алгоритм расчета
1. Определение параметров
- Выявите первый член прогрессии (a₁)
- Определите знаменатель прогрессии (q)
- Установите количество членов (n) для конечной прогрессии
- Проверьте условие |q| < 1
2. Пример расчета для конечной прогрессии
- Дано: a₁ = 100, q = 0.5, n = 5
- Расчет: S₅ = 100(1 - 0.5⁵)/(1 - 0.5)
- Результат: S₅ = 100(1 - 0.03125)/0.5 = 193.75
Особые случаи
| Ситуация | Решение |
| q = 1 | Прогрессия не является убывающей |
| |q| ≥ 1 | Сумма бесконечной прогрессии не существует |
| Отрицательный знаменатель | Формулы работают при |q| < 1 |
3. Пример расчета для бесконечной прогрессии
- Дано: a₁ = 200, q = 0.2
- Расчет: S = 200/(1 - 0.2) = 200/0.8
- Результат: S = 250
Практическое применение
- Финансовые расчеты (амортизация, дисконтирование)
- Физические процессы (затухающие колебания)
- Биологические модели (размножение организмов)
Правильное применение формул для убывающей прогрессии позволяет точно рассчитывать суммы последовательностей в различных областях науки и практической деятельности. Для сложных случаев рекомендуется использовать специализированное программное обеспечение.
