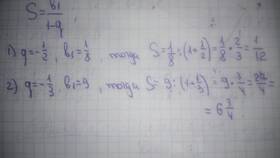Вычисление суммы первых элементов последовательности - распространенная задача в математике и программировании. Рассмотрим различные методы решения этой задачи.
Содержание
Математические подходы
| Тип последовательности | Формула суммы первых n элементов |
| Арифметическая прогрессия | Sₙ = n/2 × (2a₁ + (n-1)d) |
| Геометрическая прогрессия | Sₙ = a₁ × (1 - rⁿ)/(1 - r) при r ≠ 1 |
| Натуральный ряд | Sₙ = n(n+1)/2 |
Программные реализации
На языке Python:
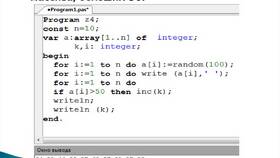
- Использование цикла for:
sum = 0
for i in range(1, n+1):
sum += i - С использованием встроенной функции:
sum(range(1, n+1)) - Через формулу для натурального ряда:
n*(n+1)//2
В Excel:
- Для арифметической прогрессии:
=n/2*(2*a1+(n-1)*d) - Для геометрической прогрессии:
=a1*(1-r^n)/(1-r) - Для произвольного диапазона:
=СУММ(A1:An)
Примеры вычислений
| Последовательность | Сумма первых 5 элементов |
| 2, 4, 6, 8, 10,... | 30 |
| 1, 3, 5, 7, 9,... | 25 |
| 1, 2, 4, 8, 16,... | 31 |
Практическое применение
Где используется:
- Финансовые расчеты (накопления, кредиты)
- Анализ временных рядов
- Статистические вычисления
- Компьютерные алгоритмы
Оптимизация вычислений:
- Используйте аналитические формулы вместо циклов
- Применяйте мемоизацию для рекурсивных вычислений
- Используйте векторные операции в математических пакетах
- Для больших n применяйте логарифмические преобразования
Ошибки и их решение
| Проблема | Решение |
| Переполнение при больших n | Использовать библиотеки для работы с большими числами |
| Накопление погрешности | Применять алгоритмы компенсации погрешности |
| Бесконечные ряды | Устанавливать точность вычислений |